민코프스키 공간

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

민코프스키 공간은 1907년 헤르만 민코프스키가 전자기학의 맥스웰 방정식과 특수 상대성 이론을 설명하기 위해 도입한 개념이다. 시간과 공간을 통합한 4차원 시공간으로, 비 유클리드 기하학이 수학 외 분야와 연관된 최초의 사례이다. 민코프스키 공간은 계량 부호수가 (-+++) 또는 (+---)인 4차원 실수 벡터 공간으로, 로렌츠 변환에 의해 불변하는 민코프스키 내적을 갖는다. 이 공간은 특수 상대성 이론의 시공간을 나타내는 틀로 사용되며, 일반화된 형태로 곡률을 갖는 로렌츠 다양체로 확장된다.

더 읽어볼만한 페이지

헤르만 민코프스키 - 민코프스키 거리
민코프스키 거리는 n차원 공간에서 두 점 사이의 거리를 정의하는 일반화된 방법으로, p값에 따라 맨해튼 거리, 유클리드 거리, 체비셰프 거리 등을 포함하며, 기계 학습에서 데이터 유사성 비교에 활용된다.
헤르만 민코프스키 - 민코프스키 정리
민코프스키 정리는 격자, 볼록집합, 대칭 조건을 만족하는 집합이 특정 부피 조건을 만족하면 격자점을 갖는다는 정리이며, 수론, 암호학 등 다양한 분야에 활용된다.
민코프스키 시공간 - 세계선
세계선은 시공간에서 물체의 경로를 나타내는 개념으로, 물체의 역사와 궤적을 시각적으로 보여주며 다양한 물리 이론과 철학적 논쟁에서 중요한 역할을 한다.
민코프스키 시공간 - 고유 시간
고유 시간은 시공간에서 물체가 실제로 경험하는 시간 간격으로, 세계선을 따라 적분한 값으로 계산되며 로렌츠 변환에 대해 불변하는 양으로, 상대성 이론에서 시간 간격을 정의하고 쌍둥이 역설과 같은 상대론적 효과를 설명하는 데 사용된다.
로런츠 다양체 - 중력 특이점
중력 특이점은 일반 상대성이론에서 시공간이 정의되지 않고 물리량이 무한대로 발산하는 지점으로, 다양한 형태로 나타나며 이론에 따라 존재가 부정되거나 사건 지평선 뒤에 숨겨져 있다고 여겨지기도 하고 블랙홀의 엔트로피와 관련된 호킹 복사 이론과도 관련된다.
로런츠 다양체 - 펜로즈 그림
펜로즈 그림은 로저 펜로즈가 도입한 시공간 도표로, 점근적으로 평탄한 시공간을 표현하기 위해 거리를 축소하는 방식을 사용하여 시공간의 인과 구조를 유계 영역으로 표현하고 블랙홀과 같은 복잡한 시공간을 묘사하는 데 활용된다.

민코프스키 공간
기본 정보
유형	시공간
차원	4차원
부호수	(-, +, +, +)
계량 텐서	η = diag(-1, 1, 1, 1)
등장	특수 상대성 이론 평탄한 시공간
수학적 구조
군	푸앵카레 군
시공간 구조	로렌츠 다양체
관련 개념
관련 개념	상대성 이론 시공간 로렌츠 변환 클리포드 대수 스피너 쌍곡 기하학

2. 역사

헤르만 민코프스키는 1907년 특수 상대성 이론을 설명하기 위한 수학적 틀로서 민코프스키 공간을 도입했다.^[34] 처음에는 전자기학의 맥스웰 방정식을 연구하는 과정에서 시작되었으나, 알베르트 아인슈타인의 특수 상대성 이론 발표 이후 자신의 연구가 이 이론을 기하학적으로 가장 잘 표현할 수 있음을 깨달았다. 이는 특수 상대성 이론 자체가 맥스웰 방정식과 기존의 갈릴레이 변환 사이의 불일치를 해결하려는 시도에서 비롯되었기 때문이다.

민코프스키는 1908년 강연에서 시간과 공간을 별개로 보는 관념은 사라지고, 오직 둘이 결합된 시공간 통일체만이 독립적인 실체로 남을 것이라고 선언하며 다음과 같이 말했다.^[35]

> 공간과 시간에 관해 내가 여기서 전개하고 싶은 시점은, 실험 물리학의 토양에서 싹튼 것이며, 그 강인함을 안에 가지고 있다. 이 시점은 혁신적인 것이며, 이제부터 공간 그 자체라든지 시간 그 자체라든지 하는 개념은 그림자에 불과한 곳으로 사라져 갈 것이다. 그리고 이 둘을 합한 것만이 독립된 실재로서 남을 것이다.

이러한 시공간 개념은 시간과 공간을 기하학적으로 통합한 최초의 시도였으며, '시공간의 비 유클리드 기하학'이라는 새로운 관점을 제시하며 물리학의 패러다임 전환을 이끌었다. 또한, 민코프스키 공간은 약 100년간 수학 내부에 머물던 비 유클리드 기하학이 처음으로 수학 외부의 물리 현상과 깊은 연관성을 맺게 된 중요한 사례이기도 하다.

초기에 알베르트 아인슈타인은 민코프스키의 접근 방식에 대해 "불필요한 박식함"이라며 회의적인 반응을 보였다.^[36] 그러나 이후 일반 상대성 이론을 연구하면서 중력장을 설명하기 위해 시공간의 기하학적 구조가 필수적임을 깨닫고 민코프스키의 업적을 높이 평가하게 되었다. 실제로 일반 상대성 이론에서 시공간은 국소적으로 민코프스키 공간과 유사한, 휘어진 시공간으로 다루어진다.

2. 1. 민코프스키 공간의 등장

1907년 독일 수학자 헤르만 민코프스키가 도입하였다.^[34] 민코프스키는 처음에는 전자기학의 맥스웰 방정식에 적합한 수학적 틀을 만들고자 연구를 시작했으나, 특수 상대성 이론이 발표되면서 자신의 연구가 특수 상대성 이론을 가장 잘 설명할 수 있는 형식임을 깨달았다. 이는 특수 상대성 이론 자체가 맥스웰 방정식과 갈릴레이 변환 사이의 모순을 해결하는 과정에서 중요한 단서들을 제공했기 때문에 우연만은 아니었다.

민코프스키의 연구 이전에, 1905년 앙리 푸앵카레는 그의 두 번째 상대성 이론 논문에서^[6] 시간을 허수 좌표 ''ict'' (여기서 ''c''는 빛의 속도, ''i''는 허수 단위)로 다루면 로렌츠 변환을 4차원 유클리드 공간의 회전으로 시각화할 수 있음을 보였다. 이 4차원 시공간에서 각 점은 하나의 사건을 나타내며, 로렌츠 변환은 이 공간에서의 회전으로 해석될 수 있다. 푸앵카레는 이 아이디어를 통해 공간 좌표의 제곱합과 허수 시간 좌표 제곱의 합(x² + y² + z² + (ict)²)이 일정하게 유지됨을 보였다. 공간 단위 벡터와 시간 단위 벡터로 이루어진 평면에서의 "회전"은 형식적으로는 좌표 공간에서의 회전이지만, 물리적 시공간에서는 실수의 관성 좌표를 가진 로렌츠 부스트이다. 이러한 회전은 쌍곡선 공간에서의 회전으로 이어진다 (쌍곡선 회전 참조).

푸앵카레가 간략하게 제시했던 이 아이디어는 1908년 민코프스키에 의해 상세히 발전되었다.^[7] 민코프스키는 맥스웰 방정식을 4개의 변수 (''x'', ''y'', ''z'', ''ict'')를 사용하여 대칭적인 방정식으로 재구성하고, 로렌츠 변환 하에서의 불변성을 명확하게 보였다. 그는 이 과정에서 처음으로 행렬 표기법을 사용하기도 했다. 이러한 재구성을 통해 민코프스키는 시간과 공간이 동등하게 다루어져야 한다는 결론에 이르렀고, 이는 통일된 4차원 시공간 연속체 개념으로 이어졌다.

1908년 "공간과 시간"이라는 제목의 강연에서 민코프스키는 허수 시간 좌표 대신 실수 시간 좌표를 사용하여 이 개념을 다시 설명했다. 그는 4차원 실수 벡터 공간에서 공간과 시간의 네 변수 (''x'', ''y'', ''z'', ''t'')를 좌표로 사용하여 시공간을 표현했다. 이 공간의 점들은 시공간의 사건에 해당한다. 이 공간에서 각 점과 관련된 광원뿔이 정의되어 있으며, 광원뿔에 있지 않은 사건은 정점과의 관계에 따라 '공간형' 또는 '시간형'으로 분류된다. 현재는 시공간에 대한 이러한 관점이 주를 이루고 있다.

민코프스키는 시간과 공간을 분리해서 보던 기존의 관념은 사라지고, 시공간 통일체만이 독립적인 실체로 남을 것이라고 주장했다.^[35] 이는 시간과 공간을 기하학적으로 통합한 첫 시도였으며, '시공간의 비유클리드 기하학'이라는 새로운 관점을 제시하여 물리학의 패러다임을 바꾸고 인류가 시공간을 더 깊이 이해하도록 이끌었다. 또한, 민코프스키 공간은 비 유클리드 기하학이 수학 외 분야와 깊은 연관성을 맺은 최초의 사례이기도 하다. 민코프스키의 주요 도구 중 하나는 민코프스키 다이어그램으로, 이를 사용하여 로렌츠 변환의 개념(고유 시간, 길이 수축 등)을 정의하고 설명했으며, 뉴턴 역학을 상대론적 역학으로 확장하는 데 기하학적 해석을 제공했다.

민코프스키는 자신의 연구가 갖는 중요성을 다음과 같이 강조했다.

> 제가 여러분께 제시하고자 하는 공간과 시간에 대한 견해는 실험 물리학의 토양에서 생겨났으며, 여기에 그들의 힘이 있습니다. 그것들은 급진적입니다. 이제부터 공간 자체와 시간 자체는 단순한 그림자로 사라지게 될 것이며, 둘의 일종의 결합만이 독립적인 현실을 보존할 것입니다.^[8]

민코프스키의 업적이 처음 알려졌을 때, 알베르트 아인슈타인은 이를 "불필요한 박식함"이라며 회의적인 시각을 보였다.^[36] 그러나 이후 일반 상대성 이론을 연구하면서 민코프스키의 기하학적 접근 방식이 필수적임을 깨닫게 되었다. 실제로 일반 상대성 이론에서 시공간은 휘어진 민코프스키 시공간으로 간주된다. 아인슈타인은 민코프스키의 접근이 중력 현상을 설명하지 못하는 한계가 있음을 인지했지만^[9], 이는 이후 곡선 좌표와 리만 기하학 연구를 통해 극복되었다. 평탄한 민코프스키 시공간은 일반 상대성 이론에서 곡선 시공간이 국소적으로 로렌츠적인 성질을 가지므로 여전히 중요한 기초로 사용된다.

수학적으로 민코프스키 공간은 1890년대에 발전한 쌍곡 4원수 개념과 관련이 있다. 민코프스키 공간은 쌍곡 4원수 공간에서 곱셈 정보를 제외하고 쌍선형 형식 ''η''(''p'', ''q'') = −(''pq''* + (''pq''*)*)/2 (쌍곡 4원수의 곱 ''pq''*에 의해 정의됨)만을 고려한 것으로 볼 수 있다.

2. 2. 복소 민코프스키 공간 (푸앵카레의 기여)

1905년 앙리 푸앵카레는 그의 두 번째 상대성이론 관련 논문에서^[6] 시간을 허수 성분을 가진 네 번째 시공간 좌표 `ict`로 다루는 방법을 제안했다. 여기서 `c`는 빛의 속도이고 `i`는 허수 단위이다. 이 방식을 사용하면 로렌츠 변환을 4차원 유클리드 구에서의 일반적인 회전으로 시각화할 수 있음을 보였다. 4차원 시공간은 각 점이 시공간에서의 사건을 나타내는 4차원 공간으로 생각할 수 있다. 로렌츠 변환은 이 4차원 공간에서의 회전으로 해석될 수 있으며, 회전축은 두 관찰자 사이의 상대 운동 방향에 해당하고 회전 각도는 그들의 상대 속도와 관련된다.

이 개념을 이해하기 위해 시공간에서 사건의 좌표를 4-벡터 `(t, x, y, z)`로 나타낼 수 있다. 로렌츠 변환은 이 4-벡터에 작용하여 그 성분을 바꾸는 행렬로 표현될 수 있다. 이 행렬은 4차원 공간에서 특정 축을 중심으로 4-벡터를 회전시키는 회전 행렬로 볼 수 있다. 푸앵카레는 이러한 변환이 다음 양을 불변으로 유지함을 보였다.

x² + y² + z² + (ict)² = 상수

두 공간 단위 벡터로 이루어진 평면에서의 회전은 좌표 공간과 물리적 시공간 모두에서 유클리드 회전으로 나타나며 일반적인 의미로 해석된다. 반면, 공간 단위 벡터와 시간 단위 벡터로 이루어진 평면에서의 '회전'은 형식적으로는 좌표 공간에서의 회전이지만, 물리적 시공간에서는 실수 관성 좌표를 가진 로렌츠 부스트에 해당한다. 유클리드 회전과의 유추는 구의 반지름이 실제로는 허수이기 때문에 부분적이며, 이는 회전을 쌍곡선 공간에서의 회전으로 바꾼다(쌍곡선 회전 참조).

푸앵카레가 잠시 언급했던 이 아이디어는 1908년 헤르만 민코프스키가 발표한 독일어 논문 "움직이는 물체 내의 전자기 과정에 대한 기본 방정식"에서 더 자세히 설명되었다.^[7] 민코프스키는 맥스웰 방정식을 네 개의 변수 `(x, y, z, ict)`와 재정의된 전자기 양에 대한 벡터 변수를 사용하여 대칭적인 방정식 형태로 재구성했다. 이를 통해 그는 로렌츠 변환 하에서의 불변성을 직접적이고 매우 간단하게 보여줄 수 있었다. 또한 그는 이 과정에서 처음으로 행렬 표기법을 사용하는 등 중요한 기여를 했다. 이러한 재구성을 통해 민코프스키는 시간과 공간을 동등하게 다루어야 한다는 결론에 이르렀고, 이는 통일된 4차원 시공간 연속체에서 사건이 발생한다는 그의 개념으로 이어졌다.

2. 3. 실수 민코프스키 공간

1908년 강연 "공간과 시간"에서 헤르만 민코프스키는 허수 시간 좌표 대신 실수 시간 좌표를 사용하여 시공간 개념을 재구성했다.^[34] 이는 4차원 실수 벡터 공간에서 공간과 시간의 네 변수 (''x'', ''y'', ''z'', ''t'')를 좌표 형태로 나타낸 것이다. 이 공간의 점들은 시공간의 사건에 해당하며, 각 점과 관련된 광원뿔이 정의된다. 광원뿔 밖에 있는 사건은 정점과의 관계에 따라 '공간형' 또는 '시간형'으로 분류된다.

현재 시공간에 대한 이러한 관점이 주를 이루고 있으며, 일반 상대성 이론에서도 평탄한 민코프스키 시공간은 곡선 시공간이 국소적으로 로렌츠적이기 때문에 중요한 기초로 사용된다.

민코프스키 논문의 영어 번역본에서는 민코프스키 계량을 '선 요소'로, 직교성('정규성') 개념을 사용했으며, 민코프스키 노름 제곱은 "합"으로 언급되었다.

민코프스키의 주요 도구는 민코프스키 다이어그램이었는데, 이를 사용하여 로렌츠 변환의 개념(예: 고유 시간, 길이 수축)을 정의하고 설명했으며, 뉴턴 역학을 상대론적 역학으로 일반화하는 데 기하학적 해석을 제공했다. 시공간 간격의 불변성은 푸앵카레 군을 시공간의 대칭군으로 하는 수학적 구조의 기초가 된다.

민코프스키는 자신이 수행한 이론의 근본적인 재진술을 인식하고 다음과 같이 말했다.

: 제가 여러분께 제시하고자 하는 공간과 시간에 대한 견해는 실험 물리학의 토양에서 생겨났으며, 여기에 그들의 힘이 있습니다. 그것들은 급진적입니다. 이제부터 공간 자체와 시간 자체는 단순한 그림자로 사라지게 될 것이며, 둘의 일종의 결합만이 독립적인 현실을 보존할 것입니다.^[8]

민코프스키가 물리학에 중요한 발전을 이루었지만, 알베르트 아인슈타인은 그 한계를 보았다.

: 민코프스키가 유클리드 3차원을 시간을 포함하는 유사 유클리드 4차원으로 확장하여 특수 상대성 이론에 대한 기하학적 해석을 제시했을 때, 아인슈타인은 이미 이것이 유효하지 않다는 것을 알고 있었습니다. 왜냐하면 이것이 중력 현상을 배제하기 때문입니다. 그는 아직 곡선 좌표와 리만 기하학 연구에 미치지 못했고, 그에 수반되는 무거운 수학적 장치도 있었습니다.^[9]

3. 구조

민코프스키 공간은 계량 부호수가 $(-,+,+,+)$ 인 비퇴화 쌍선형 형식이 갖추어진 4차원 실수 벡터 공간이다. 때로는 $(+,−,−,−)$ 를 부호수로 사용하기도 한다. 이는 k = 3인 4차원 유사 유클리드 공간과 같다. 민코프스키 공간은 계량 부호수를 강조하여 '''R'''^1,3으로 나타내거나, '''M'''⁴ 또는 간단히 '''M'''으로 표기하기도 한다.

민코프스키 공간의 원소는 사건 또는 사차원 벡터라고 불린다. 이 공간은 준 리만 다양체 중에서 가장 간단한 예시 중 하나이다.

더 일반적으로, (''m'',''n'')-형 민코프스키 공간 $\mathbf{M}^{m,n}$ 은 계량을 고려하지 않으면 ''m''-차원 유클리드 공간 $\mathbf{E}^m$ 과 ''n''-차원 유클리드 공간 $\mathbf{E}^n$ 의 가군 직합으로 정의된다: $\mathbf{M}^{m,n} = \mathbf{E}^m \oplus \mathbf{E}^n$ . 이는 집합으로는 데카르트 곱 $\mathbf{M}^{m,n} = \mathbf{E}^m \times \mathbf{E}^n$ 과 같으며, 벡터 공간의 연산(덧셈, 스칼라 곱)이 각 성분별로 정의된다. 이 공간의 차원은 $m+n$ 이다.

('''m'',''n'')-형 민코프스키 공간 $\mathbf{M}^{m,n} = \mathbf{E}^m \times \mathbf{E}^n$ 에서의 민코프스키 계량 $\eta_{(m,n)}$ 은 각 유클리드 공간의 계량 $d_{(m)}, d_{(n)}$ 을 사용하여 두 벡터 $V = (V_{(m)}, V_{(n)})$ 와 $W = (W_{(m)}, W_{(n)})$ 에 대해 다음과 같이 정의된다.

$\eta_{(m,n)}(V,W) = d_{(m)}(V_{(m)},W_{(m)}) - d_{(n)}(V_{(n)},W_{(n)})$

벡터 $V$ 의 노름 제곱은 다음과 같다.

$V^2 = \eta_{(m,n)}(V,V) = (V_{(m)})^2 - (V_{(n)})^2$

이 민코프스키 계량은 양수가 아닌 노름 제곱 값을 가질 수 있으므로, 양의 정부호가 아닌 부정 부호 계량이다. 예를 들어, $V = (\mathbf{0}_{(m)}, V_{(n)})$ 형태의 벡터는 노름 제곱이 $V^2 = - (V_{(n)})^2 \le 0$ 이 된다.

3. 1. 민코프스키 내적

민코프스키 공간의 원소는 '''사건''' 또는 사차원 벡터라고 불린다. '''M'''을 4차원 실수 벡터 공간이라 할 때, 민코프스키 내적은 유클리드 공간의 내적과 유사하지만, 상대성이론과 관련된 다른 기하학을 기술하기 위해 차이가 있다. 민코프스키 내적은 계량 부호수가

(-,+,+,+)

또는

(+,−,−,−)

인 비퇴화 쌍선형 형식이다. 이는 다음 성질을 만족하는 사상 η: ''M'' × ''M'' → '''R''' (즉, 주어진 공간 '''M'''의 임의의 두 벡터 '''v''', '''w'''에 대해 실수를 주는 함수 η('''v''','''w'''))이다.^[18]

임의의 실수 a와 민코프스키 공간의 벡터 ''u'', ''v'', ''w''에 대해, 민코프스키 내적은 다음 속성을 만족한다.

속성	설명
쌍선형성	η(au + v, w) = aη(u, w) + η(v, w) η(u, av + w) = aη(u, v) + η(u, w)
대칭성	η(v,w) = η(w,v)
비겹침성 (비퇴화성)	모든 w ∈ M에 대해 η(v,w) = 0 이면 v = 0.

민코프스키 내적은 양의 정부호가 아니기 때문에 엄밀히 말해 내적이 아니다. 즉, 벡터 '''v'''의 '''민코프스키 노름 제곱''' ||'''v'''||² = η('''v''','''v'')는 0이 아닌 벡터 '''v'''에 대해서도 양수일 필요가 없다 (음수이거나 0일 수 있다). 양의 정부호 조건은 비겹침성으로 대체되며, 이러한 내적은 indefinite^영어 (부정) 내적이라고 한다.

유클리드 공간에서처럼, 두 벡터 '''v''', '''w'''가 η('''v''', '''w''') = 0 을 만족하면 두 벡터는 직교한다고 한다. 민코프스키 공간에는 η('''v''', '''v''') ≤ 0 이고 η('''w''', '''w''') ≥ 0 (또는 그 반대)인 벡터들이 직교하는 쌍곡 직교성 개념도 존재한다.

민코프스키 공간에서 단위 벡터는 η('''v''','''v''') = ±1 을 만족하는 벡터 '''v'''를 말한다. 상호 직교하는 단위 벡터로 구성된 민코프스키 공간의 기저는 정규 직교 기저라 불린다.^[19] 실베스터의 관성 법칙에 따라, 민코프스키 내적 공간은 항상 정규 직교 기저를 가지며, 어떤 기저에서든 양의 단위 벡터(η(e,e)=+1)와 음의 단위 벡터(η(e,e)=-1)의 수는 고정되어 있다. 이 수의 쌍(양수 개수, 음수 개수)을 내적의 '''부호수'''라 한다. 민코프스키 공간의 부호수는 관례에 따라 $(+,−,−,−)$ 또는 $(−,+,+,+)$ 를 사용한다.

민코프스키 계량 η는 민코프스키 공간의 계량 텐서이며, 유형 (0,2)의 비퇴화 대칭 쌍선형 형식이다. 두 벡터 u, v를 인수로 받아 실수 η(u, v)를 반환하며, 이를 "민코프스키 내적" 또는 "상대론적 점곱"이라고도 부른다.

$u \cdot v = \eta(u,\, v)$

두 인수가 같을 경우,

$u \cdot u = \eta(u, u) \equiv \|u\|^2 \equiv u^2,$

결과 값은 "민코프스키 노름 제곱"이라고 한다.

내적과 노름 제곱의 중요한 특징은 로렌츠 변환에 대해 불변이라는 점이다. 즉, 로렌츠 변환 Λ에 대해 다음이 성립한다.

$\eta(\Lambda u, \Lambda v) = \eta(u, v)$

특수 상대성 이론의 공준과 시공간의 균질성, 공간의 등방성으로부터, 두 사건 $(t_1, x_1, y_1, z_1)$ 과 $(t_2, x_2, y_2, z_2)$ 사이의 시공간 간격의 제곱 $(\Delta s)^2$ 은 좌표계에 의존하지 않는 불변량이다. 부호수 $(+,−,−,−)$ 를 사용하면 다음과 같다.^[20]

$(\Delta s)^2 = c^2(t_1 - t_2)^2 - (x_1 - x_2)^2 - (y_1 - y_2)^2 - (z_1 - z_2)^2.$

이 이차 형식은 분극 항등식을 통해 쌍선형 형식인 민코프스키 내적을 정의하는 데 사용될 수 있다.

부호수 $(+,−,−,−)$ 를 기준으로, 민코프스키 공간의 표준 기저(정규 직교 기저)는 서로 직교하는 네 개의 벡터 집합 $\{e_0, e_1, e_2, e_3\}$ 이며, 다음을 만족한다.

$\eta(e_0, e_0) = 1, \quad \eta(e_1, e_1) = \eta(e_2, e_2) = \eta(e_3, e_3) = -1$

$\eta(e_\mu, e_\nu) = 0 \quad (\mu \neq \nu)$

이 조건은 계량 텐서의 성분 $\eta_{\mu \nu}$ 를 사용하여 다음과 같이 간결하게 쓸 수 있다.

$\eta(e_\mu, e_\nu) = \eta_{\mu \nu}$

여기서 $\eta_{\mu \nu}$ 는 다음과 같은 행렬의 성분이다.

$\eta = (\eta_{\mu \nu}) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}$

(만약 부호수 $(−,+,+,+)$ 를 사용한다면, $\eta_{00} = -1, \eta_{11} = \eta_{22} = \eta_{33} = 1$ 이 된다.)

표준 기저에 대해 벡터 $v$ 의 성분은 $(v^0, v^1, v^2, v^3)$ 로 쓰며, 아인슈타인 표기법을 사용하여 $v = v^\mu e_\mu$ 로 나타낸다. 성분 $v^0$ 는 $v$ 의 '''시간 성분'''이라 하고, 나머지 세 성분 $(v^1, v^2, v^3)$ 은 '''공간 성분'''이라 하며, 3차원 벡터 $\mathbf{v} = (v^1, v^2, v^3)$ 로 식별될 수 있다.

성분으로 나타내면, 두 벡터 $v$ 와 $w$ 사이의 민코프스키 내적은 다음과 같다. (부호수 $(+,−,−,−)$ 기준)

$\eta(v, w) = \eta_{\mu \nu} v^\mu w^\nu = v^0 w^0 - v^1 w^1 - v^2 w^2 - v^3 w^3$

지표 내리기를 사용하여 공변 성분 $v_\mu = \eta_{\mu \nu} v^\nu$ 를 정의하면 ( $v_0 = v^0, v_1 = -v^1, v_2 = -v^2, v_3 = -v^3$ ), 내적은 다음과 같이 표현할 수도 있다.

$\eta(v, w) = v_\mu w^\mu = v^\mu w_\mu = v_0 w^0 + v_1 w^1 + v_2 w^2 + v_3 w^3$

벡터 $v$ 의 민코프스키 노름 제곱은 다음과 같다.

$\|v\|^2 = \eta(v, v) = \eta_{\mu \nu} v^\mu v^\nu = (v^0)^2 - (v^1)^2 - (v^2)^2 - (v^3)^2 = v^\mu v_\mu$

두 개의 시간꼴 벡터 $u_1$ 과 $u_2$ 가 같은 시간 방향을 가질 때 (즉, 둘 다 미래 방향 또는 둘 다 과거 방향), 그 내적은 다음의 역 코시-슈바르츠 부등식을 만족한다.^[12]

$\eta(u_1, u_2) \ge \| u_1 \| \| u_2 \|$

등호는 두 벡터가 선형 종속일 때 성립한다. 부호수 $(+,−,−,−)$ 를 사용하여 대수적으로 표현하면:

$u_1^0 u_2^0 - \mathbf{u}_1 \cdot \mathbf{u}_2 \ge \sqrt{((u_1^0)^2 - \mathbf{u}_1^2) ((u_2^0)^2 - \mathbf{u}_2^2)}$

여기서 $\mathbf{u}_1 \cdot \mathbf{u}_2 = u_1^1 u_2^1 + u_1^2 u_2^2 + u_1^3 u_2^3$ 는 3차원 공간 성분의 스칼라곱이다. 이 부등식으로부터 같은 방향의 시간꼴 벡터들의 내적은 항상 양수임을 알 수 있다 ( $\|u_1\|$ 과 $\|u_2\|$ 는 시간꼴 벡터의 정의에 의해 양의 실수이다).

3. 2. 표준 기저

민코프스키 공간의 표준 기저는 서로 직교하는 네 개의 벡터

(\mathbf e_0, \mathbf e_1, \mathbf e_2, \mathbf e_3)

로 이루어진다. 이 벡터들은 다음 조건을 만족시킨다.

:

-(\mathbf{e}_0)^2 = (\mathbf{e}_1)^2 = (\mathbf{e}_2)^2 = (\mathbf{e}_3)^2 = 1

이 조건은 민코프스키 내적

\langle \cdot, \cdot \rangle

과 메트릭 텐서

\eta_{\mu\nu}

를 사용하여 더 간결하게 표현할 수 있다. 여기서

\mu, \nu

는 (0, 1, 2, 3) 중 하나의 값을 가지는 인덱스이다.

:

\langle \mathbf{e}_\mu , \mathbf{e}_\nu \rangle = \eta_{\mu\nu}

계량 부호수를

(-,+,+,+)

로 사용하는 경우, 메트릭 텐서

\eta

는 다음과 같은 행렬로 표현된다.

:

\eta = \begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}

(간혹

(+, -, -, -)

부호수를 사용하기도 하며, 이 경우

\eta

행렬의 부호가 반대가 된다.)

이 표준 기저를 이용하여 임의의 사차원 벡터

\mathbf v

는 성분

(v^0, v^1, v^2, v^3)

으로 나타낼 수 있다. 아인슈타인 표기법을 사용하면

\mathbf v = v^\mu \mathbf e_\mu

와 같이 간결하게 표현할 수 있다. 여기서

v^0

성분은 벡터

\mathbf v

의 '''시간적 성분'''이라 하고, 나머지 세 성분

(v^1, v^2, v^3)

은 '''공간적 성분'''이라고 부른다. 공간적 성분은 종종 3차원 벡터

\mathbf{v} = (v^1, v^2, v^3)

로 나타내기도 한다.

두 벡터

\mathbf{v}

와

\mathbf{w}

의 민코프스키 내적은 성분을 이용하여 다음과 같이 계산할 수 있다. (아인슈타인 표기법 사용)

:

\langle \mathbf{v} , \mathbf{w} \rangle = \eta_{\mu\nu}v^\mu w^\nu = - v^0 w^0 + v^1 w^1 + v^2 w^2 + v^3 w^3

마찬가지로 벡터

\mathbf v

의 민코프스키 노름의 제곱은 다음과 같다.

:

||\mathbf{v}||^2 = \langle \mathbf{v} , \mathbf{v} \rangle = \eta_{\mu\nu}v^\mu v^\nu = - (v^0)^2 + (v^1)^2 + (v^2)^2 + (v^3)^2

3. 3. 시간꼴 벡터의 속성

시간꼴 벡터는 빛의 속도보다 작은 속도로 (0, 0, 0, 0) 지점의 관찰자가 도달할 수 있는 사건을 나타내므로 상대성 이론에서 특별한 중요성을 가진다. 시간꼴 벡터의 흥미로운 특징은 유사하게 방향을 가진다는 점인데, 이는 모든 시간꼴 벡터가 미래(전진) 광원뿔 또는 과거(후진) 광원뿔 중 하나에 속한다는 것을 의미한다. 이러한 벡터들은 공간꼴 벡터와는 구별되는 몇 가지 고유한 속성을 지닌다. 이는 미래 광원뿔과 과거 광원뿔이 모두 볼록 집합인 반면, 공간꼴 영역은 볼록하지 않기 때문에 나타나는 특징이다.

두 개의 시간꼴 벡터

u_1 = (t_1, x_1, y_1, z_1)

과

u_2 = (t_2, x_2, y_2, z_2)

의 스칼라 곱은 다음과 같이 정의된다.

\eta (u_1, u_2) = u_1 \cdot u_2 = c^2 t_1 t_2 - x_1 x_2 - y_1 y_2 - z_1 z_2 .

중요한 속성 중 하나는 같은 방향을 가진 두 시간꼴 벡터의 스칼라 곱은 항상 양수라는 것이다. 이는 아래에서 설명할 역 코시-슈바르츠 부등식으로부터 유도될 수 있다. 만약 두 벡터의 스칼라 곱이 0이라면, 적어도 둘 중 하나는 널 벡터이거나 공간꼴 벡터여야 한다. 반대로, 두 공간꼴 벡터의 스칼라 곱은 양수, 음수 또는 0이 될 수 있다. 예를 들어, 공간 성분이 서로 직교하고 시간 성분의 부호가 같거나 다른 두 공간꼴 벡터의 곱을 생각해보면 이를 확인할 수 있다.

시간꼴 벡터의 스칼라 곱 양수성 덕분에, 같은 방향을 가진 시간꼴 벡터들의 양의 계수를 사용한 선형 결합 역시 같은 방향의 시간꼴 벡터가 된다는 것을 쉽게 알 수 있다. 이는 벡터 합이 광원뿔의 볼록성 때문에 항상 광원뿔 내부에 머무르기 때문이다.

시간꼴 벡터

u = (ct, x, y, z)

의 노름(크기)은 다음과 같이 정의된다.

\left\| u \right\| = \sqrt{ \eta(u, u) } = \sqrt{c^2 t^2 - x^2 - y^2 - z^2}

광원뿔의 볼록성에서 파생되는 또 다른 중요한 결과는 역 코시-슈바르츠 부등식이다.^[12] 서로 다른 두 개의 유사하게 방향을 가진 시간꼴 벡터

u_1

과

u_2

에 대해 이 부등식은 다음과 같이 표현된다.

\eta(u_1, u_2) > \left\| u_1 \right\| \left\| u_2 \right\|

이를 대수적으로 풀어서 쓰면 다음과 같다.

c^2 t_1 t_2 - x_1 x_2 - y_1 y_2 - z_1 z_2 > \sqrt{\left(c^2 t_1^2 - x_1^2 - y_1^2 - z_1^2\right) \left(c^2 t_2^2 - x_2^2 - y_2^2 - z_2^2\right)}

이 부등식을 통해 스칼라 곱의 양수성을 다시 한번 확인할 수 있다.

같은 방향을 가진 두 시간꼴 벡터

u

와

w

에 대해, 역 삼각 부등식은 다음과 같이 성립한다.^[13]

\left\| u + w \right\| \ge \left\| u \right\| + \left\| w \right\|,

여기서 등호는 두 벡터가 선형 종속 관계일 때 성립한다.

이 부등식의 증명은 역 코시-슈바르츠 부등식을 이용하여 대수적으로 다음과 같이 이루어진다:^[14]

\begin{align}\left\| u + w \right\| ^2&= \eta(u+w, u+w) \\&= \eta(u, u) + 2 \eta(u, w) + \eta(w, w) \\&= \left\| u \right\|^2 + 2 \eta(u, w) + \left\| w \right\|^2 \\&\ge \left\| u \right\| ^2 + 2 \left\| u \right\| \left\| w \right\| + \left\| w \right\|^2 \quad (\because \text{역 코시-슈바르츠 부등식 } \eta(u, w) \ge \|u\| \|w\|) \\&= \left( \left\| u \right\| +  \left\| w \right\|  \right)^2.\end{align}

양변에 제곱근을 취하면 원하는 부등식

\left\| u + w \right\| \ge \left\| u \right\| + \left\| w \right\|

을 얻는다.

4. 인과 구조

민코프스키 공간에서 두 사건 사이의 관계는 두 사건을 잇는 4차원 벡터의 성질에 따라 결정된다. 벡터는 그 고유한 길이(정확히는 길이의 제곱에 해당하는 민코프스키 내적 값)의 부호에 따라 시간 유사(timelike), 공간 유사(spacelike), 영 벡터(null vector) 또는 빛 유사(lightlike)로 분류된다.^[10] 시간 유사는 두 사건 간에 인과적 연결이 가능함을, 공간 유사는 인과적 연결이 불가능함을, 영 벡터는 빛의 속도로 연결됨을 의미한다. 이 분류는 관찰자의 움직임 상태가 변해도(즉, 로렌츠 변환을 해도) 바뀌지 않는다.

한 사건을 기준으로 모든 영 벡터들의 집합은 그 사건의 광원뿔을 형성한다. 광원뿔은 시공간을 그 사건의 인과적 미래(영향을 줄 수 있는 영역), 인과적 과거(영향을 받은 영역), 그리고 그 외(인과적으로 무관한 영역)로 나눈다.

시간 방향(과거에서 미래로 흐르는 방향)을 정하면^[11], 시간 유사 벡터와 영 벡터는 각각 미래 방향과 과거 방향으로 더 세분화될 수 있다. 예를 들어, 미래 방향 시간 유사 벡터는 현재 사건에서 미래의 어떤 사건으로 향하는, 빛보다 느린 속도의 움직임을 나타낸다. 이러한 벡터 분류와 광원뿔 구조는 민코프스키 공간의 기본적인 인과 구조를 형성하며, 어떤 사건이 다른 사건의 원인이나 결과가 될 수 있는지를 결정하는 기준이 된다.

4. 1. 시간적, 공간적, 영 벡터

민코프스키 공간의 벡터는 그 민코프스키 내적 ''η''(''v'', ''v'')의 부호에 따라 분류된다. 물리학에서는 주로 두 가지 부호 규약, (-, +, +, +) 또는 (+, -, -, -)가 사용된다. 여기서는 주로 사용되는 (-, +, +, +) 규약을 따른다. 즉, 4차원 벡터 ''v'' = (''ct'', ''x'', ''y'', ''z'') = (''ct'', '''r''')에 대해 내적은 ''η''(''v'', ''v'') = -(''ct'')² + ''x''² + ''y''² + ''z''² = -(''ct'')² + '''r'''² 로 계산된다.

벡터 ''v''는 다음과 같이 분류된다.^[10]

시간적(time-like): ''η''(''v'', ''v'') < 0 (즉, '''r'''² < (''ct'')²)일 경우. 이는 두 사건 사이에 인과 관계가 성립할 수 있음을 의미하며, 시간 간격이 공간 간격보다 크다. 예를 들어, 물체의 세계선을 따라 이동하는 변위 벡터는 시간적이다.
공간적(space-like): ''η''(''v'', ''v'') > 0 (즉, '''r'''² > (''ct'')²)일 경우. 이는 두 사건 사이에 인과 관계가 성립할 수 없음을 의미하며, 공간 간격이 시간 간격보다 크다. 한 관찰자에게는 동시에 일어나는 사건으로 측정될 수 있다. (동시성의 상대성)
영 벡터 또는 광적(null or light-like): ''η''(''v'', ''v'') = 0 (즉, '''r'''² = (''ct'')²)일 경우. 이는 빛의 속도로 전파되는 신호와 관련된 벡터이다.

이러한 벡터의 분류는 로렌츠 변환에 대해 불변하다. 즉, 어떤 관성 좌표계에서 관측하든 벡터의 종류(시간적, 공간적, 영적)는 동일하게 유지된다.

민코프스키 공간의 한 사건에서 모든 영 벡터들의 집합은 그 사건의 광원뿔을 형성한다. 광원뿔은 과거와 미래를 가르는 경계 역할을 한다.

시간 방향을 선택하면^[11](예를 들어, 시간 좌표 ''t''가 증가하는 방향을 미래로 정의하면), 시간적 벡터와 영 벡터를 더 세분화할 수 있다. 벡터 ''v'' = (''v''⁰, ''v''¹, ''v''², ''v''³)에서 ''v''⁰ = ''ct''를 시간 성분이라고 할 때,

시간적 벡터:
'''미래 방향 시간적 벡터''': ''η''(''v'', ''v'') < 0 이고 ''v''⁰ > 0. 벡터의 끝점이 해당 사건의 미래 광원뿔 내부에 있다.
'''과거 방향 시간적 벡터''': ''η''(''v'', ''v'') < 0 이고 ''v''⁰ < 0. 벡터의 끝점이 해당 사건의 과거 광원뿔 내부에 있다.
영 벡터:
'''영벡터''': 모든 성분이 0인 벡터 (0, 0, 0, 0). (원점)
'''미래 방향 영 벡터''': ''η''(''v'', ''v'') = 0 이고 ''v''⁰ > 0. 벡터의 끝점이 미래 광원뿔 표면에 있다.
'''과거 방향 영 벡터''': ''η''(''v'', ''v'') = 0 이고 ''v''⁰ < 0. 벡터의 끝점이 과거 광원뿔 표면에 있다.

공간적 벡터를 포함하면, 민코프스키 공간의 벡터는 총 6가지 종류로 나눌 수 있다.

민코프스키 공간의 정규 직교 기저는 반드시 하나의 시간적 단위 벡터와 세 개의 공간적 단위 벡터로 구성된다. 하지만 필요에 따라 정규 직교가 아닌 기저를 사용할 수도 있으며, 예를 들어 모든 벡터가 영 벡터로 구성된 '''영 기저'''(null basis)를 구성하는 것도 가능하다.

어떤 벡터장이 그 영역의 모든 점에서 시간적, 공간적 또는 영 벡터를 가지면, 그 벡터장은 각각 시간적, 공간적 또는 영 벡터장이라고 불린다.

4. 2. 인과적 선후 관계

민코프스키 공간에서 두 사건 사이의 관계는 두 사건을 잇는 4차원 벡터의 종류에 따라 결정된다.^[10] 시간 ''t''와 3차원 공간 좌표 (''x'', ''y'', ''z'')를 이용하여 4차원 벡터 ''v'' = (''ct'', ''x'', ''y'', ''z'') = (''ct'', '''r''')를 정의할 수 있다. 여기서 ''c''는 빛의 속도이다. 이 벡터는 ''c''²''t''² − ''r''² 값의 부호에 따라 다음과 같이 분류된다.

시간 유사(timelike): ''c''²''t''² > ''r''². 두 사건 사이에 시간적인 간격이 충분히 커서 인과적으로 연결될 수 있는 경우이다.
공간 유사(spacelike): ''c''²''t''² < ''r''². 두 사건 사이의 공간적 거리가 너무 멀어 빛의 속도로도 도달할 수 없는 경우이다. 즉, 서로 영향을 줄 수 없다.
영(null) 또는 빛 유사(lightlike): ''c''²''t''² = ''r''². 빛이 이동하는 경로에 해당하는 경우이다.

이 분류는 민코프스키 내적 ''η''(''v'', ''v'')의 부호로도 표현할 수 있으며(시간 유사 < 0, 공간 유사 > 0, 영 = 0), 로렌츠 변환에 의해 기준 좌표계가 바뀌어도 변하지 않는다. 이는 로렌츠 변환에 따른 시공간 간격의 불변성 때문이다.

민코프스키 공간의 한 사건에서 모든 영 벡터들의 집합은 그 사건의 광원뿔을 형성한다. 광원뿔은 과거와 미래를 나누는 경계 역할을 한다. 시간 유사 벡터 ''v''가 주어지면, 민코프스키 다이어그램에서 직선으로 표현되는 일정한 속도의 세계선이 이와 연관된다.

시간 방향을 선택하면^[11](보통 시간 좌표 ''t'' 또는 벡터의 첫 번째 성분 ''v''⁰가 양수인 방향을 미래로 정함), 시간 유사 벡터와 영 벡터를 더 세분화할 수 있다.

시간 유사 벡터:
미래 방향 시간 유사 벡터: 첫 번째 성분(''ct'' 또는 ''V''⁰)이 양수. 벡터의 끝점이 그림의 인과적 미래(절대적 미래) 영역에 위치한다.
과거 방향 시간 유사 벡터: 첫 번째 성분이 음수. 벡터의 끝점이 인과적 과거(절대적 과거) 영역에 위치한다.
영 벡터:
영 벡터: 모든 성분이 0인 벡터 (0, 0, 0, 0). 사건 자기 자신을 나타낸다.
미래 방향 영 벡터: 첫 번째 성분이 양수. 위쪽 광원뿔(미래 광원뿔)에 해당한다.
과거 방향 영 벡터: 첫 번째 성분이 음수. 아래쪽 광원뿔(과거 광원뿔)에 해당한다.

이 분류를 이용하여 두 사건 ''x'', ''y'' ∈ ''M'' 사이의 인과적 선후 관계를 다음과 같이 정의할 수 있다.

1. ''x''가 ''y''보다 시간적으로 앞선다 (''x'' < ''y''): 벡터 ''y'' − ''x''가 미래 방향 시간 유사 벡터일 경우이다. 이는 ''x''에서 출발한 영향이 빛보다 느린 속도로 ''y''에 도달할 수 있음을 의미한다. 이 관계는 추이성을 만족한다.

2. ''x''가 ''y''보다 인과적으로 앞선다 (''x'' ≤ ''y''): 벡터 ''y'' − ''x''가 미래 방향 영 벡터 또는 미래 방향 시간 유사 벡터일 경우이다. 이는 ''x''에서 출발한 영향이 빛의 속도 또는 그보다 느린 속도로 ''y''에 도달할 수 있음을 의미한다. 즉, ''x''가 ''y''의 원인이 될 수 있다. 이 관계는 시공간의 부분 순서를 정의한다.

어떤 시간 유사 벡터 ''x'' ∈ ''M''가 주어졌을 때, ''x''에 대한 동시 초평면(simultaneity hyperplane)은 {''y'' : ''η''(''x'', ''y'') = 0}으로 정의된다. 이는 ''x''와 공간적으로 분리된 사건들의 집합, 즉 특정 관찰자(벡터 ''x''로 대표되는)에게 동시에 일어나는 것으로 간주되는 사건들의 집합이다. 그러나 이 동시 초평면은 기준 벡터 ''x''의 선택(즉, 관찰자의 속도)에 따라 달라지는데, 이는 특수 상대성이론의 중요한 결과인 동시성의 상대성을 보여준다.

5. 수학적 구조

민코프스키 공간은 4차원 실수 벡터 공간으로, 각 지점의 접선 공간에 민코프스키 내적이라고 불리는 비퇴화 대칭 쌍선형 형식 $\eta$ 를 갖추고 있다. 이 내적의 계량 부호수는 관례에 따라 $(+, -, -, -)$ 또는 $(-, +, +, +)$ 중 하나를 사용한다. 여기서는 시공간이 관성 좌표계에 해당하는 좌표계를 갖추었다고 가정하며, 이는 시공간을 벡터 공간으로 모델링하는 데 필요한 원점을 제공한다.

민코프스키 내적은 유클리드 내적과 달리 양의 정부호가 아니며 "부정부호(indefinite)"라고 불린다. 즉, 벡터 $v$ 에 대한 이차 형식 $\eta(v, v)$ 는 0이 아닌 벡터에 대해서도 음수 또는 0이 될 수 있다. 양의 정부호 조건 대신 비퇴화성(모든 벡터 $v$ 에 대해 $\eta(u, v) = 0$ 이면 $u = 0$ 이라는 조건)이 요구된다.

민코프스키 내적(또는 민코프스키 계량) ''η''는 민코프스키 공간의 계량 텐서이며, 유사 리만 계량의 한 종류이다. 이는 두 벡터 $u, v$ 를 인수로 받아 실수 값 $\eta(u, v)$ 를 반환한다. 표기법으로, 민코프스키 공간의 벡터(4-벡터)는 이탤릭체 ''v''로 표기하는 것이 일반적이다.

민코프스키 내적 $u \cdot v = \eta(u, v)$ 와 이로부터 정의되는 민코프스키 노름 제곱 $\|u\|^2 = \eta(u, u)$ 은 로렌츠 변환 하에서 불변하는 중요한 양이다. 실제로 로렌츠 변환은 민코프스키 내적을 보존하는 변환으로 정의될 수 있다.

두 벡터 $v, w$ 가 $\eta(v, w) = 0$ 을 만족하면 서로 직교한다고 한다. 벡터 $e$ 가 $\eta(e, e) = \pm 1$ 을 만족하면 단위 벡터라고 하며, 서로 직교하는 단위 벡터들로 이루어진 기저를 정규 직교 기저라고 한다.^[19] 실베스터의 관성 법칙에 따라 정규 직교 기저에서 양의 노름 제곱을 갖는 벡터 수와 음의 노름 제곱을 갖는 벡터 수는 항상 일정하다.

특수 상대성 이론의 공준에 따라, 두 사건 사이의 시공간 간격 제곱 $\Delta s^2$ 은 모든 관성 좌표계에서 불변하는 양이다.^[20] 이 간격 제곱은 두 사건의 좌표 차이 벡터 $\Delta V$ 의 민코프스키 노름 제곱 $\eta(\Delta V, \Delta V)$ 과 같다. 이 불변성은 분극 항등식을 통해 민코프스키 내적 $\eta$ 를 정의하는 데 사용될 수 있다. 표준 좌표계 $(ct, x, y, z)$ 와 부호수 $(+, -, -, -)$ 를 사용하면, 내적은 $u \cdot v = c^2 t_1 t_2 - x_1 x_2 - y_1 y_2 - z_1 z_2$ 로 표현되며, 이는 행렬 형식을 통해 계량 텐서 $\eta$ 와 연결된다.

5. 1. 접선 벡터

민코프스키 공간은 4차원 실수 벡터 공간이며, 시공간의 각 지점의 접선 공간에는 비퇴화 대칭 쌍선형 형식인 민코프스키 내적을 갖춘다. 이 내적의 계량 부호수는 (+, −, −, −) 또는 (−, +, +, +)이다. 각 사건(시공간의 점)에서의 접선 공간은 시공간과 동일한 4차원의 벡터 공간이다.

민코프스키 공간의 벡터 공간 구조는 각 점 ''p''에서의 접선 공간 ''T_pM''의 벡터를 민코프스키 공간 ''M'' 자체의 벡터(점 또는 사건)와 정식으로 식별할 수 있게 한다. 이는 모든 접선 공간을 원본 벡터 공간과 동일시하는 것과 같다. 이러한 식별은 수학에서 통용된다. (예: Lee (2003), Proposition 3.8 또는 Lee (2012), Proposition 3.13 참조) 데카르트 좌표계에서 이 식별은 다음과 같이 표현된다.^[15]

\begin{align}\left(x^0,\, x^1,\, x^2,\, x^3\right)\ &\leftrightarrow\ \left. x^0 \mathbf e_0 \right|_p + \left. x^1 \mathbf e_1 \right|_p + \left. x^2 \mathbf e_2 \right|_p + \left. x^3 \mathbf e_3 \right|_p \\&\leftrightarrow\ \left. x^0 \mathbf e_0 \right|_q + \left. x^1 \mathbf e_1 \right|_q + \left. x^2 \mathbf e_2 \right|_q + \left. x^3 \mathbf e_3 \right|_q\end{align}

여기서 ''p''와 ''q''는 임의의 두 사건(점)이고, e_μ|_''p''는 점 ''p''에서의 접선 공간 기저 벡터이다. 이 기저 벡터는 다음과 같이 정의된다.

\left.\mathbf e_\mu\right|_p = \left.\frac{\partial}{\partial x^\mu}\right|_p \quad \text{ 또는 } \quad\mathbf e_0|_p = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \text{, 등등}.

위 식별에서 두 번째 등가 관계(↔)는 점 ''p''의 기저 벡터를 점 ''q''의 기저 벡터와 동일시하는 것을 의미하며, 이는 평행 이동이라 불린다. 첫 번째 등가 관계(↔)는 임의의 점 ''p''에서의 접선 공간 벡터를 공간 ''M'' 자체의 벡터(''n''-튜플)와 정식으로 식별함을 보여준다.

접선 공간의 기저 벡터를 1차 미분 연산자(∂/∂''x''^μ)로 나타낼 수 있는 이유는, 기하학적 접선 벡터가 매끄러운 함수 집합에 대한 방향 미분 연산자와 일대일 대응 관계에 있기 때문이다. 이러한 관점은 반드시 '''R'''^''n''에 포함될 필요가 없는 일반적인 다양체에서 접선 벡터를 ''정의''하는 데 사용되기도 한다. (접선 벡터를 단순히 ''n''-튜플로 정의하는 것도 가능하다.)

다른 관점에서, 점 ''p''에서의 접선 벡터는 로렌츠 변환 Λ 하에서 좌표계 간에 변환되는 4 × 1 열 벡터 ''v''로 정의될 수도 있다. 이 벡터 ''v''는 좌표 ''x''^μ와 동일한 방식, 즉 ''v'' → Λ''v'' 규칙에 따라 변환된다. 이를 명시적으로 나타내면 다음과 같다.

\begin{align}x'^\mu &= {\Lambda^\mu}_\nu x^\nu, \\v'^\mu &= {\Lambda^\mu}_\nu v^\nu.\end{align}

이 정의는 정식 동형사상을 통해 앞서 설명한 미분 연산자로서의 정의와 동등하다.

어떤 목적에서는 점 ''p''에서의 접선 벡터를 ''p''에서의 변위 벡터와 식별하는 것이 바람직하며, 이는 본질적으로 동일한 정식 식별을 통해 가능하다.^[16] 위에 언급된 벡터의 식별은 수학적 설정뿐만 아니라, 더 물리적이고 명시적인 기하학적 설정에서도 대응하는 내용을 찾을 수 있다 (예: Misner, Thorne & Wheeler (1973) 참조).

5. 2. 계량 부호

민코프스키 공간에서 벡터들의 민코프스키 내적을 정의할 때 사용되는 계량 텐서 η는 특정 계량 부호수를 가진다. 이 부호수는 관례에 따라 두 가지 방식 중 하나로 선택된다.

가장 널리 사용되는 두 가지 부호 규약은 다음과 같다.

`(+ − − −)` 규약:
시간 성분에 양의 부호(+), 공간 성분에 음의 부호(-)를 부여한다.
계량 텐서: $\eta = \operatorname{diag}(1, -1, -1, -1)$
이 방식은 주로 입자 물리학 분야에서 선호된다. 예를 들어 란다우와 리프시츠의 저서에서 이 규약을 사용한다. 입자 물리학에서 자주 등장하는 특정 양들에서 마이너스 부호가 줄어드는 장점이 있다.
두 벡터 $v = (v^0, v^1, v^2, v^3)$ 와 $w = (w^0, w^1, w^2, w^3)$ 의 내적은 $\eta(v, w) = v^0 w^0 - v^1 w^1 - v^2 w^2 - v^3 w^3$ 로 계산된다.
벡터 $v$ 의 노름 제곱은 $\eta(v, v) = (v^0)^2 - (v^1)^2 - (v^2)^2 - (v^3)^2$ 이다.

`(− + + +)` 규약:
시간 성분에 음의 부호(-), 공간 성분에 양의 부호(+)를 부여한다.
계량 텐서: $\eta = \operatorname{diag}(-1, 1, 1, 1)$
이 방식은 주로 수학 및 일반 상대성 이론 분야에서 선호된다. 예를 들어 스티븐 와인버그의 저서에서 이 규약을 사용한다. 이 규약은 비상대론적 극한 에서 유클리드 공간의 계량 부호수 `(+, +, +)`와의 형식적 유사성을 유지하는 장점이 있다.
두 벡터 $v, w$ 의 내적은 $\eta(v, w) = -v^0 w^0 + v^1 w^1 + v^2 w^2 + v^3 w^3$ 로 계산된다.
벡터 $v$ 의 노름 제곱은 $\eta(v, v) = -(v^0)^2 + (v^1)^2 + (v^2)^2 + (v^3)^2$ 이다.

어떤 부호 규약을 선택하는지는 물리적인 결과에 영향을 미치지 않는다.^[20] 즉, 두 규약 모두 특수 상대성 이론의 기본 공준들과 일치하며, 단지 계산상의 편의나 특정 분야의 관례에 따라 선택될 뿐이다. 한 규약에서 다른 규약으로 결과를 변환하려면, 유도 과정에서 사용된 계량 텐서

\eta

를

-\eta

로 바꾸고 계산을 다시 진행하면 된다.

민코프스키 공간의 정규 직교 기저

\{e_0, e_1, e_2, e_3\}

는 선택된 부호 규약에 따라

\eta(e_\mu, e_\nu) = \eta_{\mu\nu}

관계를 만족한다. 예를 들어 `(−, +, +, +)` 규약에서는

\eta(e_0, e_0) = -1

,

\eta(e_1, e_1) = \eta(e_2, e_2) = \eta(e_3, e_3) = 1

이고,

\mu \neq \nu

일 때는

\eta(e_\mu, e_\nu) = 0

이다. 반대로 `(+, −, −, −)` 규약에서는

\eta(e_0, e_0) = 1

,

\eta(e_1, e_1) = \eta(e_2, e_2) = \eta(e_3, e_3) = -1

이고,

\mu \neq \nu

일 때는

\eta(e_\mu, e_\nu) = 0

이다.

5. 3. 용어

민코프스키 공간은 계량 부호수가

(-,+,+,+)

(또는 경우에 따라

(+,−,−,−)

)인 비퇴화 쌍선형 형식이 갖추어진 4차원 실수 벡터 공간이다.^[17] 즉, k = 3인 4차원 유사 유클리드 공간으로 볼 수 있으며, 기호로는 계량 부호수를 강조하여 '''R'''^1,3으로 나타내거나, '''M'''⁴ 또는 간단히 '''M'''으로 표기하기도 한다. 민코프스키 공간은 유사 리만 다양체의 가장 간단한 예 중 하나이다.

민코프스키 공간의 원소는 '''사건''' 또는 사차원 벡터라고 불린다. 이 공간의 수학적 구조는 시공간을 모델링하는 데 사용되며, 특히 특수 상대성 이론의 기초를 이룬다.

'''민코프스키 내적''' (또는 '''민코프스키 계량'''): 민코프스키 공간 '''M'''에 정의된 쌍선형 형식 $\eta: M \times M \rightarrow \mathbf{R}$ 이다. 이는 두 벡터 $v, w \in M$ 를 입력받아 실수 값 $\eta(v, w)$ 를 반환하며, 다음과 같은 성질을 만족한다.^[18]

민코프스키 내적은 양의 정부호가 아니기 때문에 엄밀한 의미의 내적은 아니다. 즉, 벡터

v

의 '''민코프스키 노름 제곱'''

\|v\|^2 \equiv \eta(v, v)

는 양수가 아닐 수도 있고,

v

가 영벡터가 아니더라도 0이 될 수 있다. 이러한 내적은 indefinite|부정^영어 내적이라고 한다. 민코프스키 내적(또는 계량)은 로렌츠 변환에 대해 불변하는 중요한 특징을 가진다.

'''민코프스키 계량 텐서''': 민코프스키 내적에 해당하는 계량 텐서 $\eta$ 를 의미한다. 이는 민코프스키 내적과 동일한 객체로^[17], 유사 유클리드 계량 또는 유사 리만 계량의 한 종류이며, 데카르트 좌표계에서는 상수 값을 갖는 $4 \times 4$ 행렬로 표현된다. 부호수 $(+, -, -, -)$ 를 선택하면 다음과 같이 표현된다.

\eta = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}

부호수

(-, +, +, +)

를 선택하면 이 행렬에 -1을 곱한 형태가 된다. 어떤 부호수를 사용하든 물리적인 의미는 동일하다.

'''직교성''': 유클리드 공간에서와 같이, 두 벡터 $v, w$ 가 $\eta(v, w) = 0$ 을 만족하면 서로 직교한다고 한다. 민코프스키 공간에서는 $\eta(v, v) \le 0$ 이고 $\eta(w, w) \ge 0$ (또는 그 반대)인 벡터들이 직교하는 특별한 경우, 즉 쌍곡 직교성이라는 개념이 나타난다.

'''단위 벡터''': $\eta(v, v) = \pm 1$ 을 만족하는 벡터 $v$ 를 단위 벡터라고 한다.^[19]

'''정규 직교 기저''': 서로 직교하는 단위 벡터들로 구성된 민코프스키 공간의 기저를 정규 직교 기저라고 한다.^[19] 실베스터의 관성 법칙에 따라, 어떤 정규 직교 기저에서든 양의 단위 벡터( $\eta(e, e) = +1$ )와 음의 단위 벡터( $\eta(e, e) = -1$ )의 수는 항상 일정하다. 이 양수와 음수 단위 벡터 수의 쌍을 내적의 '''부호수'''라고 한다. 특수 상대성 이론에서 사용되는 민코프스키 공간의 부호수는 보통 $(1, 3)$ (양수 1개, 음수 3개) 또는 $(3, 1)$ (양수 3개, 음수 1개)이다. 표준 좌표계 $(ct, x, y, z)$ 에서 부호수 $(+, -, -, -)$ 는 시간 좌표( $ct$ )에 양수 부호를, 공간 좌표( $x, y, z$ )에 음수 부호를 할당하는 것에 해당한다.

'''시공간 간격''': 특수 상대성 이론의 공준에 따라, 두 사건 $(ct_1, x_1, y_1, z_1)$ 과 $(ct_2, x_2, y_2, z_2)$ 사이의 시공간 간격 제곱 $\Delta s^2$ 은 모든 관성 좌표계에서 불변하는 양이다.^[20] 부호수 $(+, -, -, -)$ 를 사용하면 다음과 같이 정의된다.

\Delta s^2 = c^2(t_1 - t_2)^2 - (x_1 - x_2)^2 - (y_1 - y_2)^2 - (z_1 - z_2)^2

이 간격 제곱은 두 사건의 좌표 차이 벡터

\Delta V = (\Delta (ct), \Delta x, \Delta y, \Delta z)

의 민코프스키 노름 제곱

\eta(\Delta V, \Delta V)

과 같다.

민코프스키 공간은 수학적으로 유사 유클리드 공간의 한 예이며, 일반 상대성 이론에서 다루는 더 일반적인 로렌츠 다양체의 가장 간단한 형태(즉, 평탄한 시공간)로 볼 수 있다. 로렌츠 다양체에서는 각 점의 접공간에 민코프스키 내적과 유사한 국소적인 내적 구조(계량 텐서)가 정의되지만, 이 계량은 일반적으로 공간 위치에 따라 변한다.

5. 4. 지수 올리고 내리기

기술적으로, 비퇴화 쌍선형 형식은 벡터 공간과 그 이중 공간 사이의 사상(map)을 제공한다. 이 맥락에서 사상은 민코프스키 공간 M의 접선 공간과 M의 공변 벡터 공간 사이의 사상이다. M의 한 점에서 접선 공간과 공변 벡터 공간은 쌍대 벡터 공간이다(따라서 사건에서의 공변 벡터 공간의 차원도 4이다). 리스 표현 정리에 따라, 벡터 공간에 대한 진정한 내적과 마찬가지로 민코프스키 내적도 하나의 인수가 고정되었을 때 선형 범함수의 작용으로 표현될 수 있다.^[24]

따라서, ''v''^''μ''가 접선 공간에 있는 벡터의 성분이라면, ''η''_''μν'' ''v''^''μ'' = ''v''_''ν''는 공변 벡터 공간(선형 범함수)에 있는 벡터의 성분이다. 접선 공간의 벡터와 M 자체의 벡터를 동일시하기 때문에, 이는 대부분 무시되며 아래 첨자가 있는 벡터는 '''공변 벡터'''라고 불린다. 이러한 해석에서 공변 벡터는 (거의 항상 암묵적으로) 민코프스키 공간의 이중 공간에 있는 벡터(선형 범함수)와 동일시된다. 위 첨자가 있는 것들은 '''반변 벡터'''이다. 같은 방식으로, 접선 공간에서 공변 벡터 공간으로의 사상의 역함수는, 행렬 표현에서 ''η''의 역함수로 명시적으로 주어지며, '''지수 올리기'''를 정의하는 데 사용될 수 있다. 이 역함수의 성분은 ''η''^''μν''로 표시된다. 민코프스키 메트릭의 경우 ''η''^''μν'' = ''η''_''μν''가 성립한다. 벡터 공간과 그 이중 공간 사이의 이러한 사상은 음악적 유추에 의해 ''η''^♭ (에타 플랫, 지수 내리기) 및 ''η''^♯ (에타 샤프, 지수 올리기)로 표시될 수 있다.^[25]

반변 벡터와 공변 벡터는 기하학적으로 매우 다른 객체이다. 반변 벡터는 화살표로 생각할 수 있다. 선형 함수는 두 가지 객체, 즉 커널과 노름으로 특징지을 수 있는데, 커널은 원점을 통과하는 초평면이다. 따라서 기하학적으로 공변 벡터는 노름에 따라 간격이 달라지는 (노름이 클수록 간격이 작아짐) 초평면들의 집합으로 보아야 하며, 그중 하나(커널)는 원점을 통과한다. 공변 벡터에 대한 수학적 용어는 1-코벡터 또는 1-형식(1-form)이다 (후자는 일반적으로 코벡터 ''장''에 대해 사용된다).

문헌에서 탐구된 한 양자 역학적 유추는 드브로이 파동의 (축소 플랑크 상수로 스케일링된) 운동량 사차원 벡터와 관련하여 반변 벡터의 공변 버전을 상상하는 방법을 설명한다. 두 반변 벡터의 내적은, 다른 벡터의 반변 버전에 대한 한 벡터의 공변 버전의 작용으로 동일하게 생각될 수 있다. 그러면 내적은 화살표가 평면을 관통하는 횟수로 해석될 수 있다.^[23] 수학적 참조 문헌에서도 이러한 객체에 대한 동일한 기하학적 관점을 제공한다(하지만 관통 횟수에 대한 언급은 없을 수 있다).

전자기장 텐서는 미분 2-형식이며, 이에 대한 기하학적 설명도 관련 문헌에서 찾을 수 있다.

물론 기하학적 관점을 완전히 무시하고 순전히 형식적인 방식으로 대수적으로 접근할 수도 있다. 종종 '''지수 체조'''(index gymnastics)라고 불리는 이 형식 자체의 오랜 기간 검증된 견고성은, 벡터를 이동시키고 반변 벡터에서 공변 벡터로 또는 그 반대로(그리고 더 높은 차수의 텐서로) 변경하는 것이 수학적으로 건전함을 보장한다. 잘못된 표현은 빠르게 드러나는 경향이 있다.

쌍선형 형식

\eta:M\times M\rightarrow \mathbf{R}

이 주어지면, 벡터의 내린 버전은

\eta

의 부분 평가(partial evaluation)로 생각할 수 있다. 즉, 다음과 같은 연관된 부분 평가 맵이 존재한다:

\eta(\cdot, -):M\rightarrow M^*; v \mapsto \eta(v,\cdot).

내려진 벡터

\eta(v,\cdot)\in M^*

는 쌍대 맵

u\mapsto\eta(v,u)

이다.

\eta

의 대칭성 때문에 어떤 인수가 부분적으로 평가되는지는 중요하지 않다.

비퇴화성(non-degeneracy)은 부분 평가 맵의 단사성(injectivity)과 동치이며, 또는 동등하게 비퇴화성은 맵의 커널이 자명(trivial)함을 의미한다. 유한 차원의 경우, 여기서처럼 유한 차원 공간의 차원이 쌍대 공간의 차원과 같다는 점을 고려하면, 이것은 부분 평가 맵이

M

에서

M^*

로의 선형 동형사상임을 결론 내리기에 충분하다. 그러면 역 부분 평가 맵을 정의할 수 있다:

\eta^{-1}:M^*\rightarrow M,

이를 통해 역 계량(inverse metric)을 다음과 같이 정의할 수 있다:

\eta^{-1}:M^*\times M^* \rightarrow \mathbf{R}, \eta^{-1}(\alpha,\beta) = \eta(\eta^{-1}(\alpha),\eta^{-1}(\beta))

여기서

\eta^{-1}

의 두 가지 다른 용법은 각각 평가되는 인수로 구분할 수 있다. 이것은 지수를 올리는 데 사용될 수 있다. 좌표 기저가 사용되는 경우, 계량 ''η''⁻¹는 실제로 ''η''의 행렬 역행렬이다.

6. 일반화

민코프스키 공간은 여러 방식으로 일반화될 수 있다. 대표적으로 시공간의 차원을 4차원 이상으로 확장하거나, 곡률을 도입하여 평탄하지 않은 시공간을 다루는 경우가 있다. 또한, 복소수를 이용하여 복소 민코프스키 공간을 정의하기도 한다.

로런츠 다양체는 민코프스키 공간을 일반화한 중요한 개념 중 하나로, 시공간 차원의 수를 제한하지 않으며 곡률을 가질 수 있다. 이는 중력의 효과를 고려하는 일반 상대성 이론의 기반이 된다. 반면, 민코프스키 공간 자체는 기본적으로 4차원이며 곡률이 없는 평탄한 시공간을 나타낸다.

또한, 민코프스키 공간의 수학적 개념은 임의의 ''n'' ≥ 2 차원으로 확장될 수 있으며, 이를 일반화된 민코프스키 공간이라고 부른다. 이러한 고차원 민코프스키 공간은 끈 이론이나 M-이론과 같이 4차원 이상의 시공간을 가정하는 물리 이론에서 사용된다.

6. 1. 복소 민코프스키 공간

복소 민코프스키 공간은 ''M''_c = ''M'' ⊕ ''iM''로 정의된다.^[27] 여기서 ''M''은 4-벡터의 민코프스키 공간으로, 공간의 방향 선택과 무관한 4-속도나 4-운동량 등을 포함한다. 반면, 허수 부분 ''iM''은 각속도나 자기 모멘트와 같이 방향 전환 시 방향이 바뀌는 네 개의 의사벡터로 구성될 수 있다. 여기에 방향 전환 시 부호가 바뀌는 의사스칼라 ''i''가 도입되어, ''M''_c의 요소들은 방향 선택과 무관하게 된다.

복소 민코프스키 공간 ''M''_c에서의 내적 유사 구조는 모든 ''u'',''v'' ∈ ''M''_c에 대해 ''u'' ⋅ ''v'' = ''η''(''u'', ''v'')로 정의된다.

전자 또는 다른 스핀 ½ 입자의 상대론적 순수 스핀은 ''M''_c의 원소 ''ρ'' = ''u'' + ''is''로 설명할 수 있다. 여기서 ''u''는 입자의 4-속도이며 ''u''² = 1을 만족한다. ''s''는 4차원 스핀 벡터^[28]이며, 파울리-루반스키 의사벡터로서 ''s''² = −1 및 ''u'' ⋅ ''s'' = 0을 만족한다.

6. 2. 일반화된 민코프스키 공간

로런츠 다양체는 민코프스키 공간을 두 가지 방식으로 일반화한 개념이다. 로런츠 다양체는 시공간 차원의 총 개수가 4개(또는 2개 이상)로 제한되지 않으며, 평탄할 필요 없이 곡률을 가질 수 있다. 반면, 민코프스키 공간은 기본적으로 4차원이며 곡률이 없는 평탄한 시공간을 나타낸다.

그러나 민코프스키 공간의 수학적 개념은 4차원에 국한되지 않고, 임의의 차원으로 쉽게 확장되거나 단순화될 수 있다. 이렇게 만들어진 공간을 일반화된 민코프스키 공간이라고 부른다. 만약 ''n'' ≥ 2이면, ''n''차원 민코프스키 공간은 벡터 공간으로, 그 차원은 ''n''이며 시그니처가 (''n'' − 1, 1) 또는 (1, ''n'' − 1)인 상수 민코프스키 메트릭을 갖는다.

이러한 일반화된 민코프스키 공간은 시공간이 4차원보다 많거나 적다고 가정하는 물리 이론에서 사용된다. 대표적인 예로 끈 이론과 M-이론이 있으며, 이 이론들은 4차원보다 높은 차원의 시공간을 다룬다. 끈 이론에서는 1 + 1 시공간 차원을 갖는 등각장론이 나타나기도 한다.

또한, 드 시터 공간은 일반화된 민코프스키 공간의 부분 다양체로 표현될 수 있으며, 쌍곡 기하학의 모델 공간 역시 마찬가지 관계를 갖는다.

6. 3. 곡률

민코프스키 공간은 '''평탄한 시공간'''으로 불린다. 이는 민코프스키 시공간의 세 공간 성분이 항상 피타고라스 정리를 따르기 때문이다. 이러한 특성 때문에 민코프스키 공간은 특수 상대성 이론에 적합한 기초가 되며, 중력의 영향이 크지 않은 물리 시스템을 유한한 거리 내에서 잘 설명할 수 있다.

그러나 중력을 무시할 수 없는 상황에서는 시공간이 휘어지게 되므로, 일반 상대성 이론을 사용해야 한다. 일반 상대성 이론은 비유클리드 기하학의 수학을 사용하여 시공간을 모델링하며, 이렇게 휘어진 공간을 ''곡선 공간''이라고 부른다.

곡선 공간에서도 민코프스키 공간은 여전히 중요한 역할을 한다. 등가 원리에 따르면, 중력 특이점을 제외한 어떤 지점 주변의 아주 작은(무한소) 영역에는 국소 관성계를 설정할 수 있으며, 이 국소 영역은 민코프스키 공간으로 잘 근사될 수 있다.^[29] 더 추상적으로 표현하면, 중력이 존재하는 시공간은 각 지점에서의 접선 공간이 4차원 민코프스키 공간인, 휘어진 4차원 다양체로 설명된다. 따라서 민코프스키 공간의 구조는 일반 상대성 이론을 이해하는 데 필수적이다.

중력의 영향이 점점 약해지는 극한 상황에서는 시공간이 다시 평탄해져서, 국소적인 영역뿐만 아니라 전체적으로도 민코프스키 공간으로 간주할 수 있게 된다. 이러한 이유로 민코프스키 공간을 '평탄한 시공간'이라고 부르는 것이다.

7. 기하학

민코프스키 공간에 대한 "기하학"이라는 용어의 의미는 맥락에 따라 크게 달라진다. 민코프스키 공간은 유클리드 기하학을 따르지 않으며, 쌍곡 기하학 (음의 곡률)의 "모형 공간"과 구로 모형화된 기하학(양의 곡률)에 의해 드러나는 내재적 곡률을 가진 일반화된 리만 기하학도 따르지 않는다. 그 이유는 민코프스키 계량의 부정확성 때문이다. 특히 민코프스키 공간은 거리 공간이 아니며 리만 계량을 가진 리만 다양체도 아니다. 그러나 민코프스키 공간은 쌍곡 기하학을 산출하는 리만 계량을 부여받은 부분 다양체를 포함한다.

저차원(예: 2 또는 3) 쌍곡 기하학의 모형 공간은 유클리드 공간에서 한 차원 더 높은 공간, 즉 각각 $\mathbf{R}^3$ 또는 $\mathbf{R}^4$ 에 유클리드 계량 $\overline{g}$ 으로 등거리적으로 임베딩될 수 "없어" 시각화가 어렵다.^[30]^[31] 이에 비해, 양의 곡률을 가진 모형 공간은 한 차원 더 높은 유클리드 공간의 구이다.^[32] 쌍곡 공간은 임베딩 공간에 민코프스키 계량 $\eta$ 이 부여되면 한 차원 더 높은 공간에 등거리적으로 임베딩될 "수 있다".

$\mathbf{H}^{1(n)}_R \subset \mathbf{M}^{n+1}$ 을 쌍곡면의 상단 시트( $ct > 0$ )로 정의한다.

$\mathbf H_R^{1(n)} = \left\{\left(ct, x^1, \ldots, x^n\right) \in \mathbf M^n: c^2 t^2 - \left(x^1\right)^2 - \cdots - \left(x^n\right)^2 = R^2, ct > 0\right\}$

이는 시공간 차원 $n + 1$ 의 일반화된 민코프스키 공간 $\mathbf{M}^{n+1}$ 내에 존재한다. 이는 일반화된 로렌츠 군의 전이 표면 중 하나이다. 이 부분 다양체에서 유도된 계량은 다음과 같다.

$h_R^{1(n)} = \iota^* \eta,$

즉 포함 하에서 민코프스키 계량 $\eta$ 의 당김이며, 이는 리만 계량이다. 이 계량으로 $\mathbf{H}^{1(n)}_R$ 은 리만 다양체이다. 이는 리만 기하학의 모형 공간 중 하나이며, 쌍곡 공간의 쌍곡면 모형이다. 이는 상수 음의 곡률 $-1/R^2$ 을 가진 공간이다.^[33] 상단 지수의 1은 쌍곡 기하학의 여러 모형 공간의 열거를 나타내며, $n$ 은 그 차원을 나타낸다. $2(2)$ 는 푸앵카레 원반 모형에 해당하며, $3(n)$ 은 차원 $n$ 의 푸앵카레 반평면 모형에 해당한다.

위의 정의에서 $\iota: \mathbf{H}^{1(n)}_R \rightarrow \mathbf{M}^{n+1}$ 은 포함 사상이고, 위첨자 별표는 당김을 나타낸다. 현재의 목적은 $\mathbf{H}^{1(n)}_R$ 이 실제로 쌍곡 공간임을 입증하기 위한 준비로서 이와 유사한 연산을 설명하는 것이다.

포함, 일반 사상에 따른 공변 텐서의 당김, 일반 사상에 따른 벡터의 밀어내기에 따른 텐서의 동작

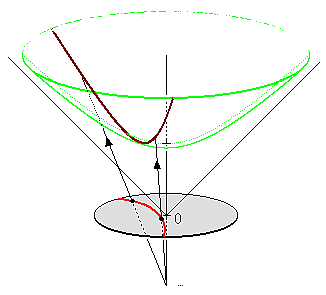
빨간색 원호는 푸앵카레 원반 모형에서 측지선이며, 녹색 쌍곡선 위의 갈색 측지선으로 투영됩니다.

계량을 나타내기 위해서는 적절한 ''매개변수화''를 통해 다시 가져와야 합니다. 다양체

M

의 부분다양체

S

의 매개변수화는

U \subset \mathbf{R}^m \rightarrow M

맵으로, 범위는

S

의 열린 부분집합입니다.

S

가

M

과 동일한 차원을 가지는 경우, 매개변수화는 좌표 맵

\phi: M \rightarrow U \subset \mathbf{R}^m

의 역입니다. 사용될 매개변수화는 ''쌍곡선 입체 투영''의 역입니다. 이는

n = 2

에 대해 오른쪽 그림에 나와 있습니다. 구에 대한 입체 투영과 비교하는 것이 도움이 됩니다.

입체 투영

\sigma: \mathbf{H}_R^n \rightarrow \mathbf{R}^n

와 그 역

\sigma^{-1}: \mathbf{R}^n \rightarrow \mathbf{H}_R^n

는 다음과 같습니다.

\begin{align}\sigma(\tau, \mathbf x) = \mathbf u &= \frac{R\mathbf x}{R + \tau},\\\sigma^{-1}(\mathbf u) = (\tau, \mathbf x) &= \left(R\frac{R^2 + |u|^2}{R^2 - |u|^2}, \frac{2R^2\mathbf u}{R^2 - |u|^2}\right),\end{align}

여기서, 편의상

\tau \equiv ct

입니다.

(\tau, \mathbf{x})

는

\mathbf{M}^{n+1}

의 좌표이고,

\mathbf{u}

는

\mathbf{R}^n

의 좌표입니다.
상세한 유도다음과 같이 정의합니다.

\mathbf H_R^n = \left\{\left(\tau, x^1, \ldots, x^n\right) \subset \mathbf M: -\tau^2 + \left(x^1\right)^2 + \cdots + \left(x^n\right)^2 = -R^2, \tau > 0\right\}

그리고

S = (-R, 0, \ldots, 0) .

만약

P = \left(\tau, x^1, \ldots, x^n\right) \in \mathbf H_R^n,

그렇다면 기하학적으로 분명한 것은, 벡터

\overrightarrow{PS}

는 초평면

\left\{\left(\tau, x^1, \ldots, x^n\right) \in M: \tau = 0\right\}

를 점

U = \left(0, u^1(P), \ldots, u^n(P)\right) \equiv (0, \mathbf u).

에서 한 번 교차한다는 것입니다.

다음이 성립합니다.

\begin{align}S + \overrightarrow{SU} &= U \Rightarrow \overrightarrow{SU} = U - S,\\S + \overrightarrow{SP} &= P \Rightarrow \overrightarrow{SP} = P - S\end{align}

또는

\begin{align}\overrightarrow{SU} &= (0, \mathbf u) - (-R,\mathbf 0) = (R, \mathbf u),\\\overrightarrow{SP} &= (\tau, \mathbf x) - (-R,\mathbf 0) = (\tau + R, \mathbf x).\end{align}.

입체 투영의 구성에 의해 다음이 성립합니다.

\overrightarrow{SU} = \lambda(\tau)\overrightarrow{SP}.

이는 방정식 시스템으로 이어집니다.

\begin{align}R &= \lambda(\tau + R),\\\mathbf u &= \lambda \mathbf x.\end{align}

이 중 첫 번째는

\lambda

에 대해 풀리고, 입체 투영의 경우 다음을 얻습니다.

\sigma(\tau, \mathbf x) = \mathbf u = \frac{R\mathbf x}{R + \tau}.

다음으로, 역

\sigma^{-1}(\mathbf{u}) = (\tau, \mathbf{x})

를 계산해야 합니다. 이전과 동일한 고려 사항을 사용하지만, 이제

\begin{align}U &= (0, \mathbf u)\\P &= (\tau(\mathbf u), \mathbf x(\mathbf u)).\end{align} ,

를 사용하여 다음을 얻습니다.

\begin{align}\tau &= \frac{R(1 - \lambda)}{\lambda},\\\mathbf x &= \frac{\mathbf u}{\lambda},\end{align}

하지만 이제

\lambda

는

\mathbf{u}

에 따라 달라집니다. 쌍곡면에 놓이는

P

의 조건은

-\tau^2 + |\mathbf x|^2 = -R^2,

또는

-\frac{R^2(1 - \lambda)^2}{\lambda^2}+\frac{|\mathbf u|^2}{\lambda^2}=-R^2,

따라서

\lambda = \frac{R^2 - |u|^2}{2R^2}.

이

\lambda

를 사용하면 다음을 얻습니다.

\sigma^{-1}(\mathbf u) = (\tau, \mathbf x) = \left(R\frac{R^2 + |u|^2}{R^2 - |u|^2}, \frac{2R^2\mathbf u}{R^2 - |u|^2}\right).

8. 로렌츠 변환

민코프스키 공간 '''M'''에서 자신으로의 변환 중 민코프스키 내적을 보존하는 것을 로렌츠 변환이라고 한다. 로렌츠 변환은 특수 상대성 이론에서 관성 좌표계 간의 변환을 나타낸다.

9. 상대론적 시공간

물리학에서 내적의 부호가 `(-, +, +, ..., +)` 또는 `(+, -, -, ..., -)`인 민코프스키 공간 `'''M'''^''d'',1` 또는 `'''M'''^{1, ''d''}`는 특수 상대성 이론에 기반한 시공간을 표현하는 틀로 사용된다. 여기서 `d`는 공간의 차원을 나타내며, 일반적인 3차원 공간에 시간을 조합한 4차원 시공간에서는 `d = 3`이다. 민코프스키 공간 `'''M'''^''d'',1` 또는 `'''M'''^{1, ''d''}`를 `'''E'''^''d''`와 `'''E'''¹`의 직합으로 분해했을 때, 부호 규약에 상관없이 `'''E'''^''d''`에 대응하는 부분은 공간 성분이라 불리고, `'''E'''¹`에 대응하는 부분은 시간 성분이라 불린다.

표준 기저를 설정할 때, `'''E'''^''d''`에 대응하는 단위 벡터는 `1, ..., d`로 번호가 매겨지고, `'''E'''¹`에 대응하는 단위 벡터는 0으로 번호가 매겨지는 경우가 많다. 이 표준 기저를 사용하여 수 벡터 공간과 동일시했을 때, 그 반변 벡터로서의 성분 표시는

$V = (V^0, V^1, \dots, V^d)$

와 같이 시간 성분을 첫 번째로 두는 경우가 많다. 공간 성분은 벡터를 볼드체로 나타내는 관습에 따라

$V = (V^0, \mathbf{V})$

로 표시되기도 한다. 때로는 시간 성분 `V`⁰을 해당 물리량의 기호로 대체하여 표기하기도 한다.

부호 규약이 `(-, +, +, ..., +)`인 경우, 두 벡터 `V`, `W`의 민코프스키 내적은 성분을 사용하여 다음과 같이 표현된다.

$\eta(V, W) = -V^0 W^0 + V^1 W^1 + \dots + V^d W^d = (\mathbf{V}, \mathbf{W}) - V^0 W^0$

여기서 `( , )`는 유클리드 공간의 표준 내적을 의미한다. 벡터 `V`의 노름 제곱은 다음과 같다.

$V^2 = \eta(V, V) = (V^1)^2 + \dots + (V^d)^2 - (V^0)^2 = \mathbf{V}^2 - (V^0)^2$

민코프스키 내적 `η`를 아인슈타인 표기법 $\eta(V, W) = \eta_{\mu\nu} V^\mu W^\nu$ 을 이용하여 행렬로 성분 표시하면 다음과 같다.

$\eta = \begin{pmatrix}-1&0&0&\cdots&0\\0&1&0&\cdots&0\\0&0&1&&0\\\vdots&\vdots&&\ddots&\vdots\\0&0&0&\cdots&1\end{pmatrix}$

이 행렬의 행렬식은 다음과 같다.

$\det \eta = -1$

반면, 부호 규약이 `(+, -, -, ..., -)`인 경우에는 민코프스키 내적 행렬이 다음과 같이 표현된다.

$\eta = \begin{pmatrix}1&0&0&\cdots&0\\0&-1&0&\cdots&0\\0&0&-1&&0\\\vdots&\vdots&&\ddots&\vdots\\0&0&0&\cdots&-1\end{pmatrix}$

이 경우 행렬식은 다음과 같다.

$\det \eta = (-1)^d$

참조

_[1] 웹사이트 Minkowski http://www.dictionar[...] 2019-06-22
_[2] 문서 This makes spacetime distance an Invariant (physics)|invariant.
_[3] 논문
_[4] 문서 Consistent use of the terms "Minkowski inner product", "Minkowski norm" or "Minkowski metric" is intended for the bilinear form here, since it is in widespread use. It is by no means "standard" in the literature, but no standard terminology seems to exist.
_[5] 서적 Independent Axioms for Minkowski Space–Time https://books.google[...] CRC Press
_[6] 논문 On the Dynamics of the Electron
_[7] 논문 The Fundamental Equations for Electromagnetic Processes in Moving Bodies
_[8] 논문 Space and Time
_[9] 문서 Einstein's Path from Special to General Relativity Clarendon Press
_[10] 문서 Translate the coordinate system so that the event is the new origin.
_[11] 문서 This corresponds to the time coordinate either increasing or decreasing when the proper time for any particle increases. An application of T flips this direction.
_[12] 문서 See Schutz's proof p 148, also Naber p. 48
_[13] 문서 Schutz p. 148, Naber p. 49
_[14] 문서 Schutz p. 148
_[15] 논문
_[16] 논문 See Lee's discussion on geometric tangent vectors early in chapter 3.
_[17] 문서 For comparison and motivation of terminology, take a Riemannian metric, which provides a positive definite symmetric bilinear form, i. e. an inner product proper at each point on a manifold.
_[18] 문서 Giulini 2008 pp. 5, 6
_[19] 서적 The Geometry of Minkowski Spacetime: An Introduction to the Mathematics of the Special Theory of Relativity https://books.google[...] Courier Corporation 2022-12-26
_[20] 서적 Spacetime and Geometry https://books.google[...] Cambridge University Press
_[21] 논문
_[22] 논문 Minkowski
_[23] 논문
_[24] 논문 One point in Lee's proof of the existence of this map needs modification (Lee deals with Riemannian metrics.). Where Lee refers to positive definiteness to show the injectivity of the map, one needs instead appeal to non-degeneracy.
_[25] 논문 The tangent-cotangent isomorphism p. 282
_[26] 논문
_[27] 웹사이트 A Physically Meaningful Relativistic Description of the Spin State of an Electron, Symmetry 2021, 13(10), 1853 https://doi.org/10.3[...] 2023-08-13
_[28] 서적 Classical Electrodynamics John Wiley & Sons: Hoboken, NJ, US
_[29] 문서 This similarity between flat space and curved space at infinitesimally small distance scales is foundational to the definition of a manifold in general.
_[30] 문서 There is an isometric embedding into ℝn according to the Nash embedding theorem (Nash 1956), but the embedding dimension is much higher, n
_[31] 논문
_[32] 논문
_[33] 논문
_[34] 논문 Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse
_[35] 논문 Raum und Zeit Physikalische Zeitschrift
_[36] 논문 Space and Time http://minkowskiinst[...] Minkowski Institute Press, Montreal 2011

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com